一致性哈希
[TOC]
普通的哈希算法,当集群节点数变更时,大部分的数据节点都会受到影响,导致原本的请求无法命中原来的节点,数据的迁移成本是非常高的。尤其是在一些 KV 分布式缓存中,者可能导致大量请求无法命中缓存。使用一致哈希实现哈希寻址可以改善这种问题,即当集群节点变更时,移除或增加节点,只有少部分节点数据收到影响。
一致哈希实现哈希寻址
一致哈希算法,将整个哈希值空间组织成一个虚拟的圆环,也就是哈希环:一致哈希算法也用了取模运算,但是一致哈希算法是对 2^32 进行取模运算,即 0~2^32 从小到大顺时针方向分布在一个圆环上。
1、比如,有3个节点 node1,node2, node3 对节点的名字(一个字符串)计算出一个 hashKey 数值,假设计算hashKey 的函数为 chash(),按大小分别放到圆环上的不同位置,这样圆环会被三个节点分成不同的区域。
2、当有一个请求 R 来时,也使用 chash() 对请求进行也计算出一个 hashKey, 然后找到在圆环上的位置,如图1 中的 R。
3、R 沿着顺时针方向找到最近的节点,也就是 node2,即请求 R 落在了 node2 上 。
4、依次类推,后续请求会落在不同的区间,顺时针就会找到不同的节点上。
5、如果有节点挂掉,比如 node2 挂了,原本请求 R 应该落在 node2 上,就会继续往后寻找,直到找到下一个节点,也就是 node3。也就是说,node2节点挂了,只会影响 node2 前面最近的一个区间的数据。其他区间不受影响。
6、如果新增一个节点 node4 如图2,请求 R 顺指针找到的节点就从 node2 变成了 node4,即增加节点也只会影响其前面最近的一个区间的数据。
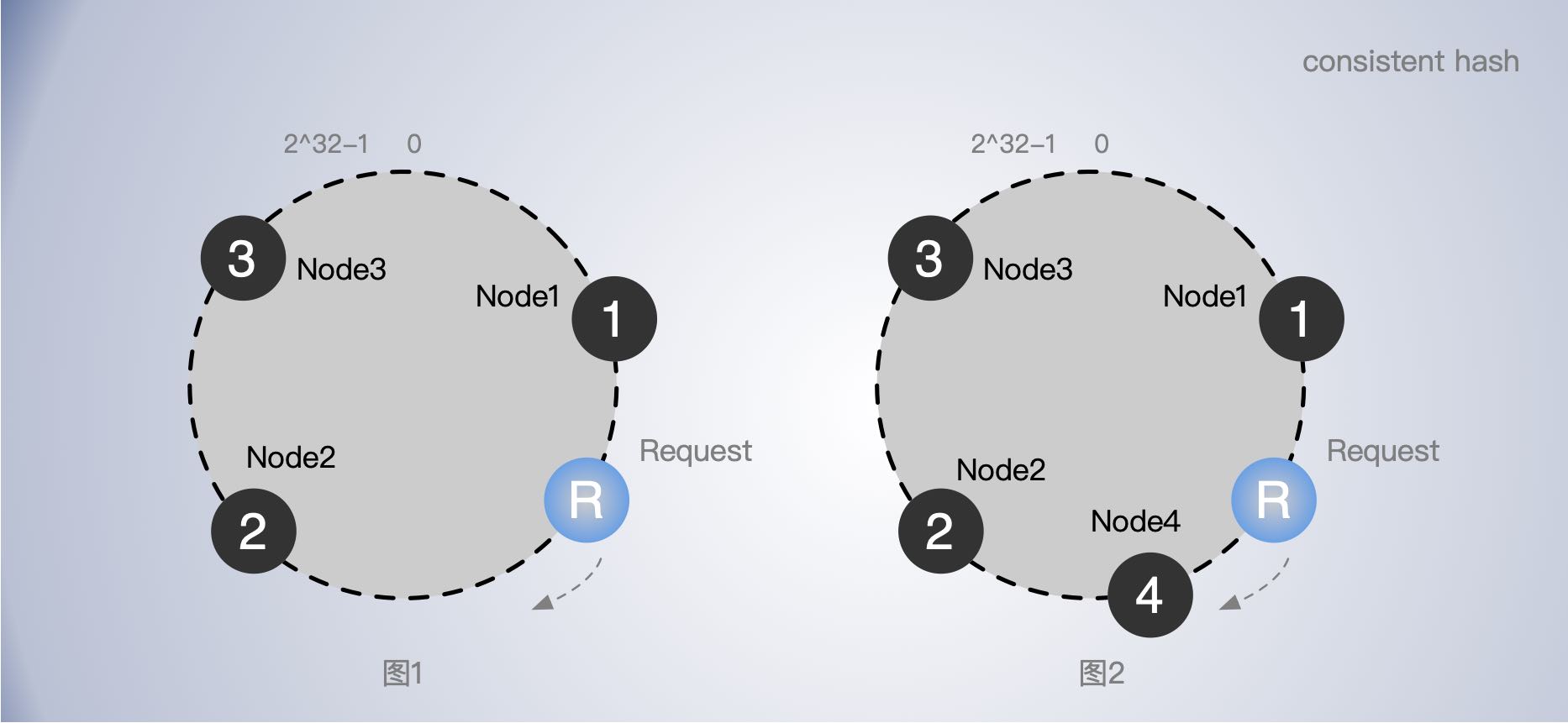
使用了一致哈希算法后,扩容或缩容的时候,都只影响变更节点前面最近的一个区间的数据。也就是说,一致哈希算法具有较好的容错性和可扩展性。
分布不均匀问题
需要注意的是,在哈希寻址中常出现的问题:落到不同的节点的请求可能分布不均匀。
在一致哈希中,如果节点太少,容易因为节点分布不均匀造成数据访问的冷热不均,即大多数访问请求都会集中少量几个节点上。
解决办法是增加虚拟节点,即对每一个服务器节点增加多个虚拟节点计算多个哈希值。比如原本的节点名为 node1,我们可以增加一些数据后缀来当作虚拟节点,如 node1-1,node1-2,node1-3 等等。这样一个 node1 节点就能分摊成多个虚拟节点落在哈希环上的不同位置。当请求落到虚拟节点上时,我们只要根据虚拟节点和真实节点的映射关系,比如保存在一个 map 里,就能找到真实的节点。
当然,如果真实节点挂了,虚拟节点对应的数据也自然会受到影响。
随着节点数越多,哈希环被分割的区间也越多,节点变更时,受影响数据的比例也越小。我们可以通过增加节点数降低节点宕机对整个集群的影响,以及故障恢复时需要迁移的数据量。
代码实现
import (
"encoding/binary"
"errors"
"fmt"
"golang.org/x/crypto/blake2b"
"hash/crc32"
"sort"
"strconv"
"sync"
)
// 一致性哈希
// 常用于对请求寻址,根据请求找服务器节点
var ErrEmptyCircle = errors.New("empty circle")
type Consistent struct {
circles map[uint32]string // 存储虚拟节点副本索引与真实节点的对应关系
nodes map[string]bool // 节点成员
nodesReplicas int // 每个节点到虚拟副本数
sync.RWMutex
sortedHashes uints // 按大小存储虚拟节点索引,通过二分查找请求命中的位置
count int64 // 总节点数
scratch [64]byte
}
// 添加哈希环节点
func (c *Consistent) Add(node string) {
c.Lock()
defer c.Unlock()
// 把 node 映射到 hash 环上
c.add(node)
}
func (c *Consistent) add(node string) {
// 记录虚拟节点与真实节点的映射关系
for i := 0; i < c.nodesReplicas; i++ {
c.circles[c.hashKey(c.replicasName(node, i))] = node
}
c.nodes[node] = true
c.updateSortedHashes()
c.count++
}
func (c *Consistent) updateSortedHashes() {
hashes := c.sortedHashes[:0]
//reallocate if we're holding on to too much (1/4th)
if cap(c.sortedHashes) > (c.nodesReplicas*4) * len(c.circles) {
hashes = nil
fmt.Println(c.sortedHashes)
}
for k := range c.circles {
hashes = append(hashes, k)
}
sort.Sort(hashes)
c.sortedHashes = hashes
}
// 根据名称计算 hashKey 数值 用于放到 hash 环上
// CRC32 实现
func (c *Consistent) hashKey1(name string) uint32 {
if len(name) < 64 {
var scratch [64]byte
copy(scratch[:], name)
return crc32.ChecksumIEEE(scratch[:len(name)])
}
return crc32.ChecksumIEEE([]byte(name))
}
// 根据名称计算 hashKey 数值 用于放到 hash 环上
// Sum512 实现
func (c *Consistent) hashKey(key string) uint32 {
out := blake2b.Sum512([]byte(key))
return binary.LittleEndian.Uint32(out[:])
}
// 节点副本名称, 名字+数字后缀
func (c *Consistent) replicasName(node string, index int) string {
return node + strconv.Itoa(index)
}
// 获取请求被映射对节点
func (c *Consistent) Get(name string) (string, error) {
c.RLock()
defer c.RUnlock()
if len(c.circles) == 0 {
return "", ErrEmptyCircle
}
key := c.hashKey(name)
// 找到请求命中的虚拟节点索引
nodeReplicasIndex := c.search(key)
// 根据虚拟节点找到真实的节点
index := c.sortedHashes[nodeReplicasIndex]
return c.circles[index], nil
}
// 使用二分查找,找到 key 应该落在那个节点区间,
// 返回区间到上限值,即请求命中点虚拟节点
func (c *Consistent) search(key uint32) (i int) {
i = sort.Search(len(c.sortedHashes), func(i int) bool {
return c.sortedHashes[i] > key
})
if i >= len(c.sortedHashes) {
i = 0
}
return
}
// 返回成员列表
func Member() {}
// 移除节点
func (c *Consistent) Remove(node string) {}
func New() *Consistent {
c := new(Consistent)
c.nodesReplicas = 100
c.circles = make(map[uint32]string)
c.nodes = make(map[string]bool)
return c
}
type uints []uint32
func (x uints) Len() int { return len(x) }
func (x uints) Less(i, j int) bool { return x[i] < x[j] }
func (x uints) Swap(i, j int) { x[i], x[j] = x[j], x[i] }
测试代码:
func TestConsistent_Get(t *testing.T) {
c := New()
c.Add("node1")
c.Add("node2")
c.Add("node3")
c.Add("node4")
c.Add("node5")
c.Add("node6")
c.Add("node7")
c.Add("node8")
c.Add("node9")
c.Add("node10")
servers := make(map[string]int)
for i := 0; i < 10000; i++ {
req := fmt.Sprintf("request_%d", i)
server, err := c.Get(req)
if s, ok := servers[server]; !ok {
servers[server] = 1
} else {
s++
servers[server] = s
}
if err != nil {
log.Fatal(err)
}
}
fmt.Println(servers)
}
采用 CRC32 计算 hashKey, 请求节点分布
// nodesReplicas = 10
map[node1:1107 node10:1218 node2:1259 node3:1222 node4:1317 node5:1332 node6:370 node7:285 node8:961 node9:929]
// nodesReplicas = 20
map[node1:463 node10:1437 node2:1374 node3:1501 node4:559 node5:1132 node6:552 node7:645 node8:1136 node9:1201]
// nodesReplicas = 100
map[node1:870 node10:1195 node2:1062 node3:1045 node4:1245 node5:958 node6:956 node7:610 node8:1141 node9:918]
采用 SUM512 计算 hashKey,请求节点分布
// nodesReplicas = 10
map[node1:1109 node10:1475 node2:770 node3:1094 node4:1151 node5:731 node6:735 node7:1023 node8:865 node9:1047]
// nodesReplicas = 20
map[node1:1122 node10:989 node2:788 node3:1031 node4:1030 node5:848 node6:860 node7:1129 node8:1218 node9:985]
// nodesReplicas = 100
map[node1:1043 node10:1005 node2:1000 node3:1095 node4:945 node5:980 node6:997 node7:965 node8:1040 node9:930]
单就请求分布均匀情况来看,后者更好。
扩展阅读
http://github.com/lafikl/consistent
https://github.com/stathat/consistent
https://ai.googleblog.com/2017/04/consistent-hashing-with-bounded-loads.html