算法与数据结构—查找
二分查找
二分查找针对的是一个有序的数据集合。每次都通过跟区间的中间元素对比,将待查找的区间缩小为之前的一半,直到找到要查找的元素,或者区间被缩小为 0。
条件与局限:
- 需要一个有序的数组,
- 由于是数组,内存必须连续,
- 数组不能有频繁的插入和删除
- 由于需要连续的内存空间,数据量不能太大。(注:4G的内存,不代表有4G的连续内存空间可用)
数组通过下标进行 O(1)的随机访问,而用链表实现则O(n)效率太低;
二分法理解起来非常简单,但是落实到代码中的边界条件要注意。
// 二分查找,循环实现
func HalfSearch(in []int, target int) int {
low := 0
high := len(in) - 1
for low <= high { // 退出循环条件
mid := low + (high - low) >> 1
switch {
case in[mid] > target: // 不相等时,需要mid往左右偏移一个单位
high = mid - 1
case in[mid] < target:
low = mid + 1
default:
return mid
}
}
return -1
}
// 二分查找,递归实现
func BinarySearch(in []int, low, high, target int) int {
if low > high {
return -1
}
mid := low + (high - low) >> 1
switch {
case in[mid] > target:
high = mid - 1
case in[mid] < target:
low = mid + 1
default:
return mid
}
return BinarySearch(in, low, high, target)
}
二分查找虽然原理极其简单,但是想要写出没有 Bug 的二分查找并不容易。
二分查找变形
- 查找第一个值等于给定值的元素
- 查找最后一个值等于给定值的元素
- 查找第一个大于等于给定值的元素
- 查找最后一个小于等于给定值的元素
// 给定一个有序数组,元素可能重复,找出第一个与目标值相等的值,返回数组index
// 找不到,返回 -1
func HalfSearchFirst(in []int, target int) int {
low := 0
high := len(in) - 1
targetIdx := -1
for low <= high { // 退出循环条件
mid := low + (high - low) >> 1
switch {
case in[mid] > target:
high = mid - 1
case in[mid] < target:
low = mid + 1
default:
// 找到目标,记录下来,看看左边还有没有了,没有则返回
targetIdx = mid
high = mid - 1 // 查找最后一个出现,只修改 low = mid + 1 即可
}
}
return targetIdx
}
// 查找第一个大于给定值
func HalfSearchFirstGt(in []int, target int) int {
low := 0
high := len(in) - 1
targetIdx := -1
for low <= high { // 退出循环条件
mid := low + (high - low) >> 1
switch {
case in[mid] > target:
targetIdx = mid // 找到目标,记录下来,看看右边还有没有了,没有则返回
high = mid - 1
case in[mid] <= target:
low = mid + 1
}
}
return targetIdx
}
通过右移实现求中值
mid = (low + high)/2
mid = low + ((high - low)>>1) # 效率更高些,且可防止low和high之和溢出
跳跃表(SkipList)
对链表加多级索引来提高查询效率。 支持快速的查找,插入,删除 链表的查找太慢,时间O(n); 为了提高查询效率,可以对数据(1,2,3,4,5,6,7,8,9),根据1,3,5,7,9 建立一层索引,还可以在1,3,5,7,9的基础上再提取1,5,9来建索引,一次类推。建立索引的间隔和层次根据实际出发。来达到提高查询的目的。
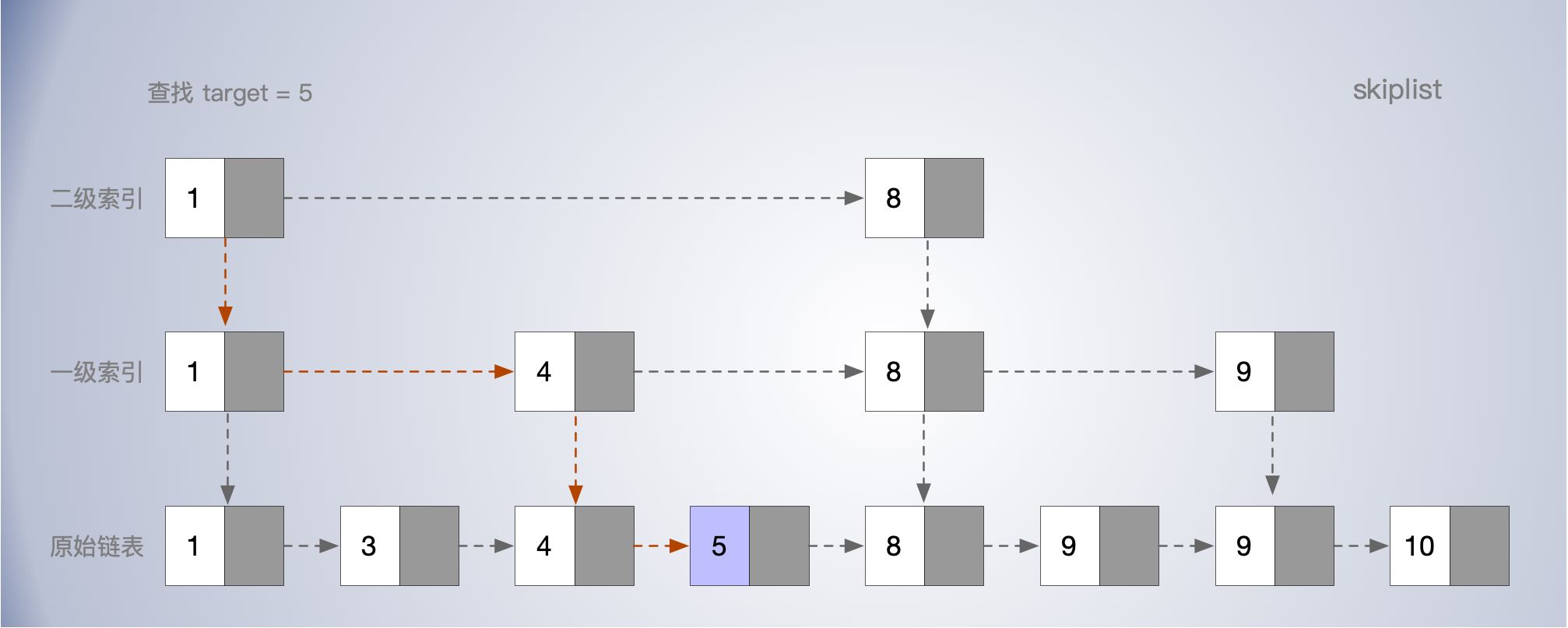
查询时间复杂度
如果建立索引的间隔为m,如果每层最多遍历m个元素,高度为logn,则时间 O(m*logn)
空间复杂度
以每2节点抽取一个索引为例,求点总数sum = n + n/2 + n/4 + n/8 + ……+8+4+2 = n-2, 故空间复杂度O(n) 可以根据查询效率和内存消耗,适当选取间隔建索引。
跳跃链表简称为跳表(SkipList),它维护了一个多层级的链表,且第i+1层链表中的节点是第i层链表中的节点的子集。跳表作为一种平衡数据结构,经常和平衡树进行比较,在大多数场景下,跳表都可以达到平衡树的效率(查询节点支持平均O(lgN),最坏O(N)的复杂度),但实现和维护起来却比平衡树简单很多。
import java.util.Random;
//跳跃表
public class SkipList {
private static final int MAX_LEVEL = 16; //跳表最大高度
private int levelCount = 1;
private Node head = new Node();
private Random r = new Random();
//层数随机产生
private int randomLevel() {
int level = 1;
for (int i = 1; i < MAX_LEVEL; i++) {
if (r.nextInt() % 2 == 1) {
level++;
}
}
return level;
}
public void insert(int value) {
Node newNode = new Node();
newNode.data = value;
int level = randomLevel();
newNode.maxLevel = level;
Node pNode = head;
int i;
//插入节点涉及更新的节点
Node[] toUpdateNode = new Node[level];
//第一个节点,需把head节点放入toUpdateNode,
for (i = 0; i < level; i++) {
toUpdateNode[i] = head;
}
//找到需要更新的节点,即每层刚好小于newNode值的节点
for (i = 0; i < level; i++) {
while (pNode.forwords[i] != null && pNode.forwords[i].data < value) {
pNode = pNode.forwords[i];
}
toUpdateNode[i] = pNode;
}
//插入新节点
for (i = 0; i < level; i++) {
newNode.forwords[i] = toUpdateNode[i].forwords[i];
toUpdateNode[i].forwords[i] = newNode;
}
//更新调表当前高度
if (level > levelCount)
levelCount = level;
}
//根据值查找节点
public void find(int target) {
int i;
Node pNode = head;
//从最高层一次往下找
for (i = levelCount - 1; i >= 0; i-- ) {
//找出每层比target刚好小的节点,然后跳到下一层继续寻找
while (pNode.forwords[i] != null && pNode.forwords[i].data < target) {
pNode = pNode.forwords[i];
}
}
if (pNode.forwords[0].data == target)
System.out.println(pNode.forwords[0]);
else
System.out.println("not found");
}
//删除特定的节点
public void delete(int target) {
//先找到要删除的节点,再删除
int i;
Node pNode = head;
//从最高层一次往下找
for (i = levelCount - 1; i >= 0; i-- ) {
//找出每层比target刚好小的节点,然后跳到下一层继续寻找
while (pNode.forwords[i] != null && pNode.forwords[i].data < target) {
pNode = pNode.forwords[i];
}
}
//后面节点覆盖前一个节点(删除)
if (pNode.forwords[0].data == target) {
pNode.forwords = pNode.forwords[0].forwords;
} else {
System.out.println("not found");
}
}
//打印出所有节点
public void printAll() {
Node pNode = head;
while (pNode != null && pNode.forwords[0] != null) {
pNode = pNode.forwords[0];
System.out.println(pNode);
}
}
public class Node {
private int data = -1;
private Node forwords[] = new Node[MAX_LEVEL];
private int maxLevel = 0;
public String toString() {
StringBuilder builder = new StringBuilder();
builder.append("{ data: ");
builder.append(data);
builder.append("; levels: ");
builder.append(maxLevel);
builder.append(" }");
return builder.toString();
}
}
}
哈希表(hash table)
散列表用的是类似数组支持按照下标随机访问数据的特性。知道下标就可以O(1)定位对应的值.
散列表用的就是数组支持按照下标随机访问的时候,时间复杂度是 O(1) 的特性。通过散列函数把元素的键值映射为下标,然后将数据存储在数组中对应下标的位置。
散列表的装载因子 = 填入表中的元素个数 / 散列表的长度 扩容 当装载因子较大时,需要申请新的空间,把数据搬过去,搬迁时可能还需要重新计算哈希值,如果数据量很大时,可能导致变慢。 动态扩容,比如当装载因子达到某个阈值如0.75时,重新申请翻倍的空间;新数据插入新的空间,旧数据分批搬过去。(期间的查找,先找新的空间,没找到去老的空间找)
哈希函数
- 怎么选择与设计? 散列函数的设计、冲突解决办法、扩容、缩容等。
- 需要尽可能均匀的分布数据
- 不能计算复杂,开销不能大
- 关键字长度,数据特点,分布,散列表大小
- 数据分析法,根据数据特点设计哈希函数
- ASCII码进位相加,取模
哈希冲突解决
- 开放寻址法: 遇到冲突往下有找空位插入,也就可能占了别人的位置,(所以hash冲突多,哈希冲突太多就不好使了),查找则对应位置被占了,往下找,知道找到或者遇到空位。(线性探测)
- 为了查找方便,需要标记已删除的数据位置,数据存放在数组中,对cpu缓存相对友好,但是链表发冲突代价更高,装载因子不能太大,接近 1 时,就可能会有大量的散列冲突,导致大量的探测、再散列等,性能会下降很多。内存间利用率不高;由于时数组存储,也不能存储太大量的数据。
- 链表法
- 相比开发寻址,装载因子可以打点;装载因子相对可以大很多;如果存储小对象,指针占用空间比例会打点;对cpu缓存不友好;可存储的数据量更大。
- 二次探测,
哈希表的代码实现?
public class Hash {
private int size = 20;
Node<String> head = null;
Node[] hashNodes = new Node[size];
public static void main(String[] args) {
Hash hash = new Hash();
hash.insert("word");
hash.insert("world");
hash.insert("words");
hash.insert("hello");
hash.find("words");
}
public boolean insert(String s) {
int i;
char c;
int hashCode;
int sum = 0;
//计算出字符串ASCII码之和
for (i = 0; i < s.length(); i++) {
c = s.charAt(i);
sum += Integer.valueOf(c);
}
hashCode = sum % size;
Node<String> newNode = new Node<String>(s, null);
if (hashNodes[hashCode] == null) {
head = newNode;
hashNodes[hashCode] = head;
} else {
Node<String> pNode = hashNodes[hashCode];
while (pNode != null && pNode.next != null) {
pNode = pNode.next;
}
pNode.next = newNode;
}
return true;
}
public void find(String s) {
int i;
char c;
int hashCode;
int sum = 0;
//计算出字符串ASCII码之和
for (i = 0; i < s.length(); i++) {
c = s.charAt(i);
sum += Integer.valueOf(c);
}
hashCode = sum % size;
if (hashNodes[hashCode] != null) {
Node<String> pNode = hashNodes[hashCode];
while (pNode.data != s && pNode.next != null) {
pNode = pNode.next;
}
if (pNode.data == s) {
System.out.println(pNode.data);
return;
}
}
System.out.println("not found");
}
//怎么储存,怎么解决冲突,怎么让分布均匀点
//用于存储数据的节点
public class Node<T> {
private T data;
private Node<T> next;
public Node (T data, Node<T> next) {
this.data = data;
this.next = next;
}
public T getData() {
return data;
}
}
}
哈希算法
将任意长度的二进制值串映射为固定长度的二进制值串,这个映射的规则就是哈希算法
要点:
- 从哈希值不能反向推导出原始数据(所以哈希算法也叫单向哈希算法)
- 对输入数据非常敏感,哪怕原始数据只修改了一个 Bit,最后得到的哈希值也大不相同;
- 散列冲突的概率要很小,对于不同的原始数据,哈希值相同的概率非常小;
- 哈希算法的执行效率要尽量高效,针对较长的文本,也能快速地计算出哈希值。
知名应用:md5,sha,crc 全加密、唯一标识、数据校验、散列函数、负载均衡、数据分片、分布式存储。
MD5哈希值是固定的 128 位二进制串.最多能表示 2^128 个数据
二叉树
满二叉树:等边三角形,子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,
完全二叉树:叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大。 堆,就是完全二叉树.
二叉树存储
- 链式存储
- 基于数组的顺序存储
数组存储,完全二叉树,最常用的存储方式就是数组。这样可以省去指针的存储开销。
为了存储方便通常从下标1开始存储;第i个节点存在下标i处,如果父节点为a[i], 则左子节点为a[2*i], 右子节点为a[2*i+1]
如果不是完全二叉树,存储的空间利用率就不高了,更适合用链表存储。
三种遍历:就是递归的过程
- 前序遍历: 先自身,再左子树,再右子树
- 中序遍历:
就是每个节点垂直的投影到底下,从左到右的顺序;查找树的中序遍历也就是从最小到最大的顺序 - 后序遍历:先左子树,再右子树,最后遍历自身。
//完全二叉树实现
public class Binarytree {
//数组存储完全二叉树,即优先从高到低,从左往右存储
char[] bt = {'A', 'B', 'C', 'D', 'E', 'F', 'G'};
public static void main (String[] args) {
Binarytree binarytree = new Binarytree();
System.out.println(binarytree.height(1));;
}
//为了存储方便通常从下标1开始存储;第i个节点存在下标i处,如果父节点为a[i], 则左子节点为a[2*i], 右子节点为a[2*i+1]
//前序遍历, 从1开始,父节点为第i个,则左子树为第2i个,右子树为第2i+1个
public void preScan(int i) {
int n = bt.length;
if (i-1 >= n || bt[i-1] == '\0') return;
//先父节点(当前节点)
System.out.print(bt[i-1]);
//再左子树节点
preScan(2*i);
//最后右子树节点
preScan(2*i+1);
}
//中序遍历, 从1开始,父节点为第i个,则左子树为第2i个,右子树为第2i+1个
public void midScan(int i) {
int n = bt.length;
if (i-1 >= n || bt[i-1] == '\0') return;
//先左子树节点
midScan(2*i);
//再父节点(当前节点)
System.out.print(bt[i-1]);
//最后右子树节点
midScan(2*i+1);
}
//后序遍历, 从1开始,父节点为第i个,则左子树为第2i个,右子树为第2i+1个
public void afterScan(int i) {
int n = bt.length;
if (i-1 >= n || bt[i-1] == '\0') return;
afterScan(2*i);
afterScan(2*i+1);
System.out.print(bt[i-1]);
}
//递归求树的高度 根节点高度=max(左子树高度,右子树高度)+1
public int height(int i) {
int n = bt.length;
if (i-1 >= n || bt[i-1] == '\0') return 0;
int heightLeft = 0;
int heightRight = 0;
int height = 0;
heightLeft = height(2*i);
heightRight = height(2*i+1);
height = (heightRight > heightLeft ? heightRight : heightLeft) + 1;
return height;
}
}
二叉查找树
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大于这个节点的值。
左子树小于父节点,右子树大于父节点的二叉树中序遍历,单调不减
递归查找、查找、插入
删除节点:
- 如果无子节点时直接删;
- 如果有一个子节点时子节点提上来;
- 有两个子节点时,右子树最小节点提升来。(沿着右子树一直左下就是)。当然也可以接标记为删除状态,但是节点还在原位置。当然这样有点浪费空间。
//二叉查找树
type Node struct {
data int
left *Node
right *Node
}
type SearchTree struct {
head *Node
}
func (s *SearchTree) Insert(data int) {
if s.head == nil {
s.head = &Node{
data: data,
left: nil,
right: nil,
}
return
}
newNode := &Node{
data: data,
left: nil,
right: nil,
}
p := s.head
for p != nil {
switch {
case p.data >= data:
if p.left == nil {
p.left = newNode
return
}
p = p.left
default:
if p.right == nil {
p.right = newNode
return
}
p = p.right
}
}
}
// 中序遍历
func (s *SearchTree) MidScan(p *Node) {
if p.left != nil {
s.MidScan(p.left)
}
fmt.Print(p.data, " ")
if p.right != nil {
s.MidScan(p.right)
}
}
// 按层遍历
func (s *SearchTree) LayScan(nodes []*Node) {
cNodeList := make([]*Node, 0)
for _, node := range nodes {
fmt.Print(node.data, " ")
if node.left != nil {
cNodeList = append(cNodeList, node.left)
}
if node.right != nil {
cNodeList = append(cNodeList, node.right)
}
}
fmt.Println()
if len(cNodeList) > 0 {
s.LayScan(cNodeList)
}
}
随便插入几个数
func TestSearchTree_LayScan(t *testing.T) {
st := SearchTree{}
st.Insert(4)
st.Insert(3)
st.Insert(5)
st.Insert(1)
st.Insert(6)
st.Insert(100)
st.Insert(0)
st.Insert(45)
nodes := []*Node{st.head}
st.MidScan(st.head) // 中序遍历
st.LayScan(nodes) // 按层遍历
}
如图,中序遍历成底层趋势 :0 1 3 4 5 6 45 100。
按层遍历的顺序为:4 3 5 1 6 0 100 45
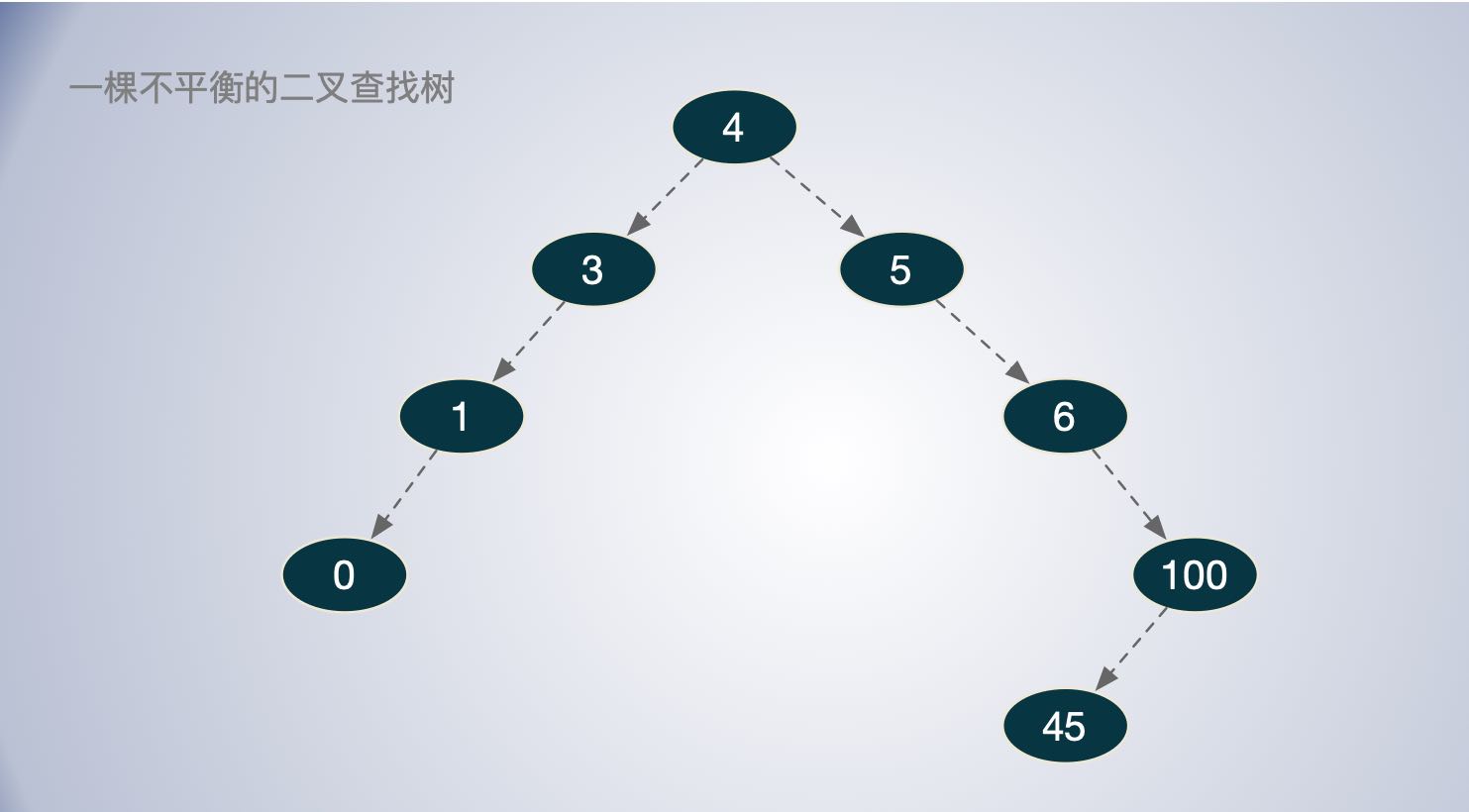
如图,这棵二叉查找树的节点数据分布很不平衡,极端情况高度远大于 logN,查找的效率也就比O(n)时间复杂度稍微好一点。
平衡二叉查找树
平衡二叉查找树中“平衡”,其实就是让整棵树左右看起来比较“对称”、比较“平衡”,不要出现左子树很高、右子树很矮的情况。实现树的高度尽可能的小,因为查找的时间与树的高度相关。
红黑树
上述的二叉查找树,可能不平衡,可能其高度远大于 logN,极端情况可能直接就是退化为链表,这样的查找效率就退化了 O(n)。而在很多地方都喜欢用红黑树。
平衡二叉查找树(近似平衡)
约束条件
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶节点(NIL节点,空节点)是黑色的。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
黑高度总是相同
由于根到每个叶子黑色节点一样多,红色节点也只能插在黑色之间且不能相邻;所以从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。从而保证了树的尽可能的平衡。
红黑树也不是完全的追求树的平衡,那样会是插入和删除的维护成本过高;红黑树是寻求查找,插入,删除,代码实现,维护成本的一个平衡。性能在各种条件下都能保持稳定。
红色节点和黑色节点都是用来存数据的,只是通过颜色标记以,数量和相邻关系来达到约束平衡的作用。
维护平衡的操作
- 改变颜色
- 左旋
- 右旋
查找: 时间复杂度:O(logn), 最差也不超过2O(logn)
插入:最多只需要2次旋转
- 每次都是在叶子上插入节点
新插入的节点必是红色,且是在叶子上,本身不会破坏约束5(根到叶子路径黑色节点数一样多)。单容易违反约束4(红色不相邻)。
情况1:插入结点z的父结点和叔父都为红色,变色即可也就是父节点和叔父红变黑,祖父黑变红即可。
情况2: 插入节点为右子树,父节点红色,叔父黑色;此时将当前节点的父结点设为新的当前节点,并以新当前节点为支点左旋。变成情况3。
情况3:插入节点为左子树,父节点红色,叔父黑色时; 父节点修改为黑色,祖父节点变为红色,并以祖父节点为支点进行右旋操作。
删除:最多3次旋转操作
除非删除叶子节点,否则就需要填补空缺;填补过程中就容易导致黑色节数点不平衡。
红黑树的第二次学习,比第一次理解多了一点,但是删除操作... 2019-04-21
红黑树是一个让人又爱又恨的数据结构,“爱”是因为它稳定、高效的性能,“恨”是因为实现起来实在太难了。
即便你将左右旋背得滚瓜烂熟,保证你过不几天就忘光了。因为,学习红黑树的代码实现,对于你平时做项目开发没有太大帮助。对于绝大部分开发工程师来说,这辈子你可能都用不着亲手写一个红黑树。除此之外,它对于算法面试也几乎没什么用,一般情况下,靠谱的面试官也不会让你手写红黑树的。
上述摘录,表示附议。。。
位图Bitmap
布尔型站1个字节,算不上很节省空间, bitmap实现:通过int,long,char类型的位运算实现。 存储1到1亿的数也就是1亿的二进制位,也就12M左右。还是很节省空间的。如果是10亿内的,就需要120M空间,如果是更大的数,那空间就会有点多了。于是有个布隆过滤器
//位图
public class Bitmap {
private int[] bytes; //申请字符数组,用于存储bitmap数据
private int nbits; //总位数
public Bitmap(int nbits) {
this.nbits = nbits;
this.bytes = new int[nbits/32+1];
}
public void set(int n) {
if (n > nbits)
return;
int byteIndex = n/32;
int bitIndex = n%32;
//a|=b;即a=a|b;按位或并赋值,按位或有一个为1则为1
bytes[byteIndex] |= (1 << bitIndex); //1 << bitIndex 表示1向左为移bitIndex位
}
public boolean get(int n) {
if (n > nbits)
return false;
int byteIndex = n/32;
int bitInex = n%32;
boolean ret = (bytes[byteIndex] & (1 << bitInex)) != 0;
return ret;
}
}
布隆过滤器 Bloom filter
bitmap的做法是根据最大的数N来申请N个二进制位。如果N很大,就不能很好的起到节省空间的目的了。
布隆过滤器的实现方式,如果最大数是10亿的话,依然用1亿个二进制位(越12M)也可能更少,但是通过哈希运算,把数N映射到1亿之内。但是冲突问题怎么解决?于是Bloom filter使用多个哈希函数把数字N,映射成多个哈希值,存储到位图中。当判断一个数是否存在时,只有经过多个哈希函数映射的值都存在时,才能认为该数N时存在的。这样可以大大降低哈希冲突的概率。
即便如此,依然还可能误判,不存在的一定不存在,存在的可能是误判,存在小概率误判。对于一些能容忍小概率误判的场景还是很有价值的。如大规模的爬虫系统,记录访问过的url。