树
[TOC]
需要掌握的
这3种遍历都有递归和循环两种不同的实现方法, 每种遍历的递归实现都比循环实现要简洁很多。
很多面试官喜欢直接或间接考查遍历。
- 树 3 种遍历的6中实现
- 宽度优先遍历,即按层遍历
-
完全二叉树,数组实现
- 二叉搜索树的面试题有很多
- 二叉树的特殊情况,堆和红黑树,红黑树相对较难,优先级往后排
三种遍历的应用场景
- 前序遍历,可以用来实现目录结构的显示。用来静态遍历访问。
- 中序遍历,对于二分搜索树,输出结果是有序递增的。
- 后续遍历,对节点操作时必访问其所有子节点,可以进行破坏性操作如删除节点。还可以计算目录内的文件占用的数据大小。
案例
重建二叉树
输入某二叉树的前序遍历和中序遍历的结果,请重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。例如输入前序遍历序列{1,2,4,7,3,5,6,8}和中序遍历序列{4,7,2,1,5,3,8,6},则重建二叉树并返回。
思路
- 前序遍历的第一个元素必是树的根节点可以确定根节点也就是 1。
- 在中序遍历中,根节点左边序列是
左子树即 {4,7,2} ,右边序列是右子树{5,3,8,6} 。 -
再根据上面两个子树的中序数字,找到对应的前序,以 {4,7,2} 为例,对应的前序就是 {2,4,7} 。
- 有了前序 {2,4,7},中序 {4,7,2} ,同样的思路,继续重复上述步骤。很明显这个很适合递归来处理了。
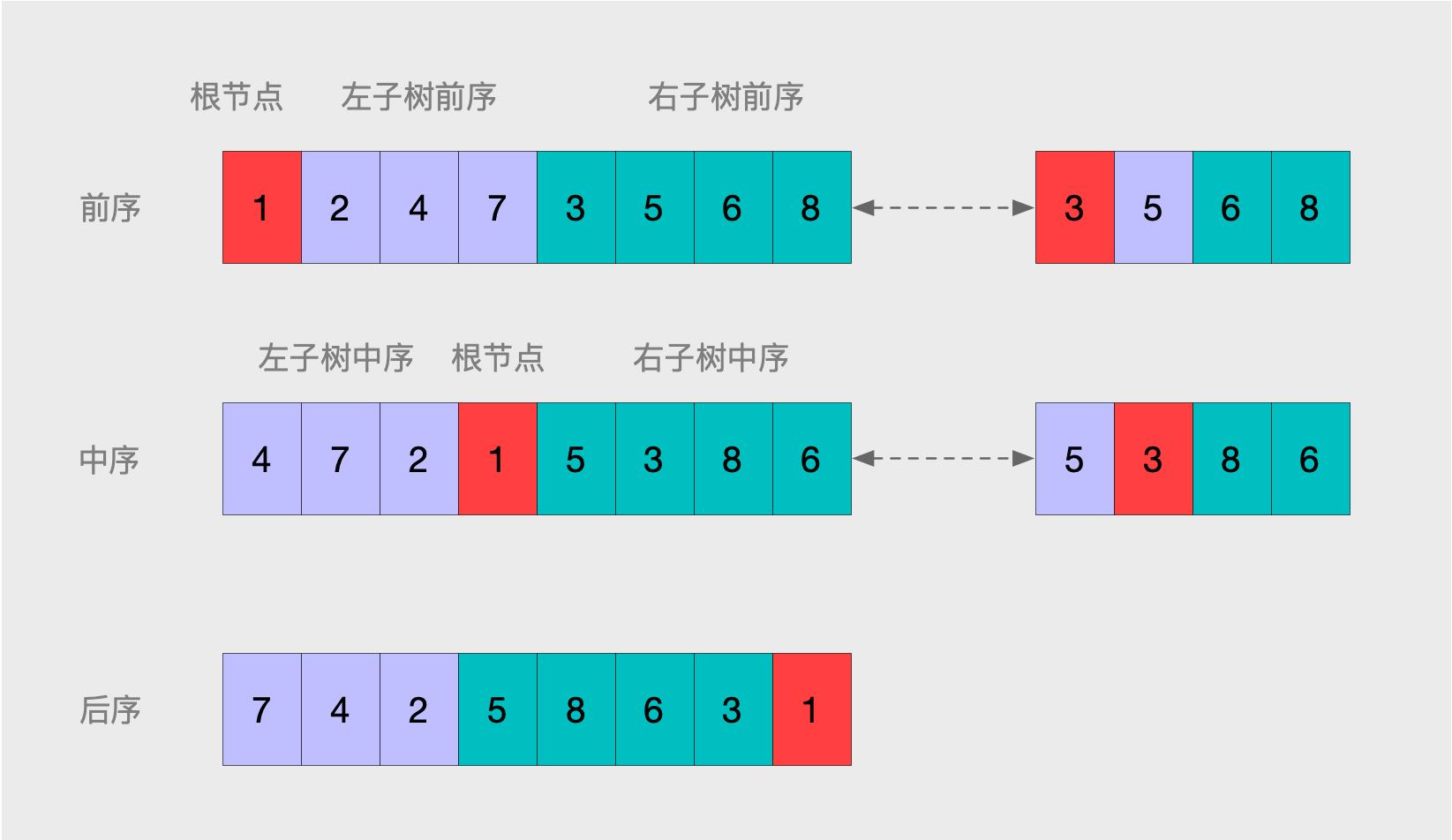
数是有一棵一棵子树组成的更大的树,无论是子树,还是完整的树,三种遍历都可以划分为[根节点,左子树,右子树]。并且再每个子树内又可以继续重复类似划分,知道没有子节点。
func ReConstructBinaryTree(pre []int, vin []int) *TreeNode {
if len(pre) == 0 || len(pre) != len(vin) {
return nil
}
if len(pre) == 1 {
return &TreeNode{
Val: pre[0],
Left: nil,
Right: nil,
}
}
root := pre[0]
leftPrev := make([]int, 0) // 左子树前序
leftVin := make([]int, 0) // 左子树中序
rightPrev := make([]int, 0) // 右子树前序
rightVin := make([]int, 0) // 右子树中序
// 找到左右子树中序
i := 0
for i < len(vin) && vin[i] != root {
leftVin = append(leftVin, vin[i])
i++
}
i++
for i < len(vin) {
rightVin = append(rightVin, vin[i])
i++
}
// 找到左右子树前序
i = 1
for ; i <= len(leftVin) && i < len(pre); i++ {
leftPrev = append(leftPrev, pre[i])
}
for ;i < len(pre); i++ {
rightPrev = append(rightPrev, pre[i])
}
// 递归构建左右子树
leftNode := ReConstructBinaryTree(leftPrev, leftVin)
rightNode := ReConstructBinaryTree(rightPrev, rightVin)
return &TreeNode{
Val: root,
Left: leftNode,
Right: rightNode,
}
}
// 用例:
// 输入为空;
// 普通二叉树,完全二叉树,只有左子树,右子树的二叉树
// 前序中序元素个数对不上;
// 只有一个元素时;只有两个,三个元素时;
// 如果输入的中序,前序,是错的,对不上;
二叉树的下一个节点
题目:给定一棵二叉树和其中的一个节点, 如何找出中序遍历序列的下一个节点?树中的节点除了有两个分别指向左、右子节点的指针,还有个指向父节点的指针。
-
如果一个节点有右子树, 那么它的下一个节点就是它的右子树中的最左子节点。即从右子节点出发一直沿着指向左子节点的指针到叶子节点。
-
如果一个节点既没有右子树, 并且它还是它父节点的右子节点。则可以沿着指向父节点的指针一直向上遍历, 直到找到一个节点是它父节点的左子节点的节点。如果这样的节点存在, 那么这个节点的父节点就是我们要找的下一个节点。
需要对二叉树有深刻的理解,考査应聘者分析复杂问题的能力。应聘者只有画出二叉树的结构图、通过具体的例子找出中序遍历下一个节点的规律, 才有可能设计出可行的算法。
试题26:树的子结构
输入两棵二叉树A,B,判断B是不是A的子结构。(ps:我们约定空树不是任意一个树的子结构)
示例1: 输入 {8,8,#,9,#,2,#,5},{8,9,#,2} , 返回 true .
func HasSubtree( pRoot1 *TreeNode , pRoot2 *TreeNode ) bool {
ret := false
if pRoot1 != nil && pRoot2 != nil {
ret = DoesTree1HasTree2(pRoot1, pRoot2)
if !ret {
ret = HasSubtree(pRoot1.Left, pRoot2)
}
if !ret {
ret = HasSubtree(pRoot1.Right, pRoot2)
}
}
return ret
}
func DoesTree1HasTree2(pRoot1 *TreeNode , pRoot2 *TreeNode ) bool {
if pRoot2 == nil {
return true
}
if pRoot1 == nil {
return true
}
if pRoot1.Val != pRoot2.Val {
return false
}
ret1 := DoesTree1HasTree2(pRoot1.Left, pRoot2.Left)
ret2 := DoesTree1HasTree2(pRoot1.Right, pRoot2.Right)
return ret1 && ret2
}
试题27:二叉树镜像
操作给定的二叉树,将其变换为源二叉树的镜像。如收入{8,6,10,5,7,9,11},变为 {8,6,10,5,7,9,11}。
思路:从根节点开始,把整个左右子树对换位置,再把左右子树当做根节点继续,重复如此。递归实现。
// 测试用例:
// 为 nil
// 只有左子树,或右子树
// 正常
func Mirror( pRoot *TreeNode ) *TreeNode {
if pRoot == nil {
return nil
}
if pRoot.Left == nil && pRoot.Right == nil {
return pRoot
}
pRoot.Left, pRoot.Right = pRoot.Right, pRoot.Left
Mirror(pRoot.Left)
Mirror(pRoot.Right)
return pRoot
}
试题28:对称的二又树
请实现一个函数,用来判断一棵二叉树是不是对称的。注意,如果一个二叉树同此二叉树的镜像是同样的,定义其为对称的。
思路一: 按层遍历二叉树,即把二叉树转化为数组存储,再求镜像,再得出镜像的数组存储的顺序,再比较前后数组是否相等。与上面的思路类似,但是少了一次遍历。注意转化为数组存储,需要填补上中间的控制接节点。
思路二:比较两棵数的前序遍历顺序是够一直。前序遍历,对称比较,先比较父级 p1 和 p2 是值否相等,再用 p1 的左右子树 和 p2 的右左子树分别比较。
// 测试用例
// 输入 nil
// 输入对称二叉树,输入不对产二叉树
func IsSymmetrical( pRoot *TreeNode ) bool {
return Symmetrical(pRoot, pRoot)
}
// 先比较父级 p1 和 p2 是值否相等,再用 p1 的左右子树 和 p2 的右左子树分别比较。
func Symmetrical(pRoot1 *TreeNode, pRoot2 *TreeNode) bool {
if pRoot1 == nil && pRoot2 == nil {
return true
}
if pRoot1 == nil || pRoot2 == nil {
return false
}
if pRoot1.Val != pRoot2.Val {
return false
}
ret1 := Symmetrical(pRoot1.Left, pRoot2.Right)
ret2 := Symmetrical(pRoot1.Right, pRoot2.Left)
return ret1 && ret2
}
试题32:从上到下打印二叉树
题目:从上往下打印出二叉树的每个节点,同层节点从左至右打印。例如输入 {5,4,#,3,#,2,#,1} ,返回 [5,4,3,2,1] 。
// 测试用例
// 输入 nil
// 只有左子树,右子树
// 只有一个节点
func PrintFromTopToBottom( root *TreeNode ) []int {
if root == nil {
return nil
}
return FromToBottom([]*TreeNode{root}, []int{})
}
func FromToBottom(pRoot []*TreeNode, nodes []int) [] int {
if len(pRoot) == 0 {
return nodes
}
children := make([]*TreeNode, 0)
for _, parent := range pRoot {
nodes = append(nodes, parent.Val)
if parent.Left != nil {
children = append(children, parent.Left)
}
if parent.Right != nil {
children = append(children, parent.Right)
}
}
return FromToBottom(children, nodes)
}